Matrix Multiplication and its Various Properties
Matrix is an important concept in the subject of mathematics and is very useful in our everyday real lives. In a layman’s language, we can define a matrix as the arrangement of different numbers or elements in a rectangular box consisting of various rows and columns. We can have an infinite number of rows and columns of a given matrix. We can carry out various arithmetic operations like addition, subtraction, multiplication, and division on matrices. In this article, we will learn in detail about matrix multiplication and discuss the various important applications of a matrix.
What Do You Mean by Matrix Multiplication?
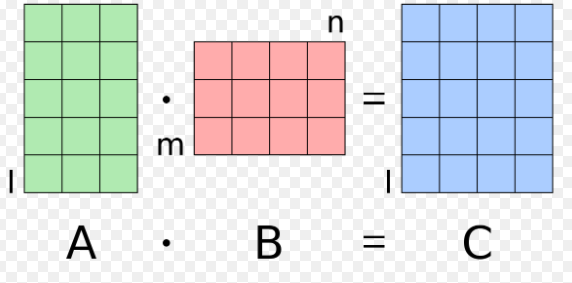
When one matrix is multiplied by the other matrix, the arithmetic operation is known as matrix multiplication. Matrix multiplication is possible only when both the matrices that are to be multiplied are compatible. After performing the compatibility test, matrix multiplication can be carried on. To check the compatibility of matrices, we need to observe their rows and columns.
For the multiplication of two matrices:
The number of rows of the second matrix = number of columns of the first matrix.
The order of the matrix X is m * n and the order of the matrix Y is n * p. We observe that the number of columns of the matrix X is equal to the number of rows of the matrix Y i.e. n = n. Thus, we will have the product of these matrices as XY of the order m * p.
Some Important Properties of Matrix Multiplication
In linear algebra, there are various properties of matrix multiplication which are discussed as follows:
- Matrix multiplication does not follow the commutative property i.e. in the case of multiplication of two matrices X and Y, XY is not equal to YX.
- The distributive property applies to the matrix multiplication which means, the product of matrix X and matrix Y can be multiplied with matrix Z, given that X, Y, and Z are compatible for the operation of multiplication.
- Matrix multiplication also follows the associative property i.e. the multiplication of AB and C and the multiplication of AC and B fetches the same result.
Important Applications of Matrices
- Matrices are very useful in cryptography. Cryptography is the process of protecting data with the help of encryption so that only the relevant person gets the data and the relevant information. The process of encryption takes the help of the concept of matrices.
- Matrices have various applications in the field of science. Important concepts like quantum mechanics, electric circuits, resistor conversion, and so on take the help of the concept of matrices as well.
- Matrices are used extensively in the field of computer graphics to construct animated cartoons, architecture, and so on.
- We take the help of matrix multiplication to find out the area of a triangle.
- Various other fields where matrices are used are optics, chemistry, geology, economics, mathematics, finances, robotics, animation, signal processing, and wireless communication.
Excel in Mathematics from Cuemath
Cuemath is one of the leading live online math classes designed to help students remove their fear of the subject of math. Students at times face difficulty and confusion in understanding the concepts of math. Cuemath has one of the best teachers who focus extensively on the conceptual clarity of students by helping them relate the theoretical concepts with real-life examples. Many recreational activities like math games, math puzzles, and so on are conducted by the teachers so that the students start loving and relating to a variety of concepts of the subject. Visit Cuemath and book a free session to learn math the Cuemath way.
click here for more articles.



